

 服務熱線
服務熱線
來源: 發表時間:2015-05-05 14:30:24 點擊次數:【】
巖礦是由晶體礦物組成的,從微觀上研究晶體的破碎對研究 巖礦破碎還是有幫助的。而且,現代固體理論在礦物晶體的變形和破碎方面還是有深入的分析和認識的。
礦物晶體的基本單位是晶胞。晶胞中的質點之間存在著互作 用力,這個互作用力包括兩種力:一是質點間的相互吸引力,它 是異性靜電荷的庫侖力,它和質點間距離的f方成反比,它維系著質點不致于脫離出庫侖力的電場;二是排斥力,當兩質點充分接近時,其外圍電子云之間就產生了相互排斥的傾向,當電子軌道相互侵占時排斥更強烈,故排斥力只有在質點間距離相當近時才有顯著作用,并隨著距離縮小而急劇增大。這兩種力的綜合效果就是質點間的互作用力。在吸引力和排斥力相等時質點處于平衡狀態,在平衡位置上作前后左右的振動。
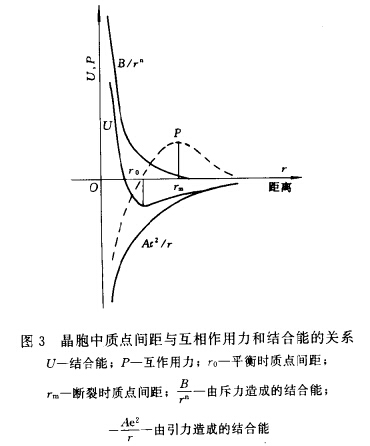
在圖3中繪出了質點間的引力、斥力和質點間距離的關系。斥 力隨距離增大而迅速減小,而當靠近時卻猛然增長。引力也是類似的變化規律,但比斥力的變化要緩和些。引力和斥力綜合形成 互作用力P,它的大小和變化如圖3中的曲線P所示。
由于質點間存在著互作用力,在構成晶體時也就具有一定的 能量,這稱為結合能(U),它的大小由下式表示:

式(14)中的第一項由引力造成,e為質點所帶電荷電量;r為質點間距離;A為麥德隆常數;第二項由斥力造成,B是和結晶構造有關的常數;指數和晶體類型有關,離子型晶體n=9~11,分子型晶體n=2~3。
圖3中的曲線U表示結合能和質點距離的關系。在吸引力和斥力相等的位置(r=r0),結合能數值最小,這就是平衡位置。增大或減小質點的距離,都將導致結合能增大,這就需要外力對它做功。質點間的互作用力P等于結合能對距離的微分:
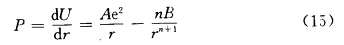
當(r=r0)時,質點處于平衡位置,P=0, U有最小的U值,代入(15)得:

將式(16)代入式(14)得:
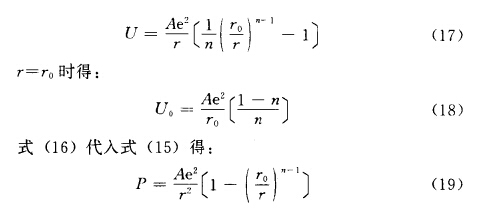
當晶體受到外力而被壓縮時,r<r0,這時斥力增大超過引力的增大,剩余的斥力支撐著外力的壓迫。當晶體受外力作用而伸張時,r<r0引力的減小少于斥力的減小,多余的引力抗御著外力的拆散作用。但隨著質點間距的進一步增加,引力的絕對值是減小的,故伸張到一定程度,當r =rm 之后(見圖3),質點間互作用力P不可能再增大了,晶體終于抵制不住外力的拉伸而被破碎。即是說,施于晶體上的外力若超過了最大可能的互作用力,晶體就被肢解了。
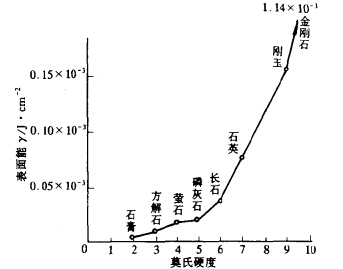
晶體在破碎之前到破碎之后,所接受的是一定的能量△U,所產生的效果是增加了若干新的表面積△S。由于居于物體表面的晶胞所具有的結合能多于中心部分的晶胞,因此晶體的表面具有表面能。表面能越大,晶體就越堅固。圖4給出了幾種標準礦物的表面能數值,金剛石在〔111〕方向的表面能是0. 114X10-2J/cm2。
在理論上晶體的表面能可以計算,礦物的強度也可以計算,但 計算得的結果偏高太多。對于玻璃、大理石和石英等典型物料,計算出的理論強度約為1010Pa,與鋼的強度相近。但實測強度僅107 或108Pa,較之理論數數級要低2~3個,即實際強度僅有理論數值的幾百分之一或幾千分之一。實測值比理論直大幅度偏低的原因,主要是因為實際的礦物晶體在結構上存在空位、錯位或加位等結構缺陷,故而破碎所需外力大幅度地降低。
晶體的破晬理論得出的結果雖然比實際偏高太多,以致不能用于指導實際的礦物晶體破碎,但它畢竟指出這樣一個道理:要使礦物晶體破碎,必須使外界施加的破碎力大于晶體的內聚力。這個道理,同樣適用于巖礦的破碎,只有當外界施加的破碎力大于巖礦塊的內聚力時才可能發生破碎。
上一篇:粗碎圓錐破碎機與顎式破碎機的比較
下一篇:篩分順序有哪幾種
